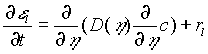 (1)
(1)Modeling of Subsurface Biobarrier Formation and Persistence
B. Chen1 and A.B. Cunningham2
1Department of Mathematics, University of Wyoming, Laramie, WY 82071, Phone: (307)766-2280, FAX:(307)766-6838; 2Center for Biofilm Engineering, Montana State University, Bozeman, MT 59717, Phone: (406)994-6109, FAX: (406)994-6098
Abstract
The purpose of this paper is to address the modeling of subsurface biobarrier formation and persistence. The modeling is first done at the microscopic scale, with a pore being represented by a tube with an expansion to take into account effects of tortuosity. The biofilm grows on the walls and changes the region of flow. This change in flow then alters the growth pattern of the bacteria. Then homogenization is used to scale up the results and obtain equations at the laboratory scale. This way we have a model at the macroscopic scale that can be used to determine how biofilm grows and its effects on porosity and permeability.
Keywords: subsurface biobarrier formation, persistence, permeability
Introduction
The use of biobarriers is a promising technology for controlling pollution in groundwater (Baker and Herson, 1994). The basic idea is to either introduce biofilm-forming bacteria into the aquifer (Characklis and Marshall, 1990) or use the bacteria already present, feed it with nutrients so the biofilm grows, and plug the media forming a biobarrier. In this way, a pollutant plume can be restricted to regions away from sources of drinking water. The basic mechanisms of biofilm growth and its relation to the flow of subsurface water, and the convection and diffusion of both contaminants and nutrients need to be understood. Work needs to be done from biological, chemical, physical, mathematical, and computational points of view.
In this paper we will deal with modeling biofilm growth at the microscopic or pore scale, and the use of homogenization to scale up the model to the laboratory scale. Macroscopic scale relations between amount of biomass and porosity and permeability are given.
Microscale model
Research has been conducted on the simulation of biofilm growth both in tubes and in porous media. In both cases the results have been on thin biofilms, that is on biofilms that cover just a small fraction of the volume of the flow region. The simulation of thick biofilms is a much more complicated problem, since the biofilm changes the flow region. We will model a pore by a straight tube with an expansion. In this way we can incorporate some of the effects of the pore geometry in our simulation. Inside the tube we assume a given initial distribution of biofilm, and a given initial flow and distribution of nutrients. As the nutrients reach the biofilm, they grow and change the geometry of the tube. These changes modify the flow pattern, which modifies the advection and diffusion of nutrients, which changes the growth of the biofilm and so on.
The biofilm model is based on Monod kinetics for the growth rate (Gujer and Wanner, 1990). We will consider a biofilm consisting of only one species of microbes and that the biofilm growth is perpendicular to the substratum. We denote this direction by h . More species can be added with much complication.
The biofilm is formed by two phases, water and bacteria. Nutrients are dissolved in water. We consider only the limiting nutrient. That is, we assume that only one nutrient limits the growth and that there are plenty of the other necessary nutrients. The relevant equations are conservation of mass for both bacteria and nutrient:
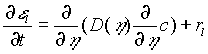 (1)
(1)
for the concentration c of the nutrient and
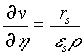 (2)
(2)
for the density r
of the bacteria. Here ![]() and
and ![]() are the local volume fractions of the biofilm occupied by the water and the microbes, respectively. D is the diffusion coefficient of the nutrient in water; t is time; v is the velocity of the bacteria; and
are the local volume fractions of the biofilm occupied by the water and the microbes, respectively. D is the diffusion coefficient of the nutrient in water; t is time; v is the velocity of the bacteria; and ![]() and
and ![]() are the rates of growth of the bacteria and decrease of the nutrient. These rates are given by Monod kinetics (Characklis and Marshall, 1990) as follows:
are the rates of growth of the bacteria and decrease of the nutrient. These rates are given by Monod kinetics (Characklis and Marshall, 1990) as follows:
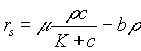 (3)
(3)
and
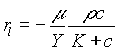 . (4)
. (4)
Here m
is the maximum specific growth rate, K the Monod saturation coefficient, b the decay coefficient, and Y the yield of bacteria per unit of nutrient. The velocity of the biofilm surface is obtained by integrating (2) and incorporating the interfacial transfer ![]() :
:
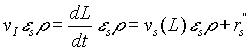 . (5)
. (5)
Here L is the position of the biofilm interface. We consider the ![]() gives the detachment of bacteria and is proportional to
gives the detachment of bacteria and is proportional to ![]() , with a negative constant of proportionality.
, with a negative constant of proportionality.
We need to solve (1) and (8) simultaneously. In order to obtain boundary conditions for (1), we need to solve for flow and transport outside the biofilm. The flow is modeled by the Navier-Stokes equations in the vorticity-stream function formulation:
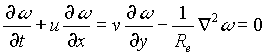 (6)
(6)
![]() , (7)
, (7)
where u and v are the velocities in the x and y directions and are given by 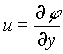 and
and 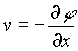 . w
is the vorticity and
. w
is the vorticity and ![]() is the Reynolds number. The transport of nutrients is modeled by the advection-diffusion equation:
is the Reynolds number. The transport of nutrients is modeled by the advection-diffusion equation:
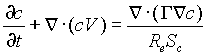 . (8)
. (8)
Here V=(u,v) the velocity vector, G
the diffusion coefficient, and ![]() the Schmidt number.
the Schmidt number.
The boundary conditions for the flow equations are no slip at solid and biofilm boundaries, Poiseuille flow at the inlet, and zero normal derivative at the outlet. For the transport, the conditions are given concentration at the inlet, zero derivative at the outlet, zero flux at solid boundaries, and continuity of the concentration and flux at biofilm interfaces. In order to avoid solving the transport equation coupled with the biofilm growth equations, we use the following iteration:
The value of the flux at the biofilm surface is assumed; the transport equation is solved; and from the solution, the value of the concentration at the surface is determined. This value is the used for solving the biofilm growth equations and a new value of the flux at the surface is obtained. This new value is used to solve the transport equation again and, we iterate, until convergence.
Equations (1) and (5)-(8) need to be solved numerically. A time-stepping procedure is implemented by replacing the time derivative with forward finite differences (Ames, 1992). The spatial derivatives are approximated by centered differences. For the integrated version of (5), the trapezoidal rule (Kinkaid and Cheney, 1991) is used to calculate the integral. At any given time, we first solve (6) and (7) to obtain the velocity. This velocity is then used in (8) and the iteration procedure described above is then used. Since the bacterial growth changes the size of the pores, at the next time step we have a different flow region. To avoid the complication and expense of regridding the region, we implement a perturbation procedure. Instead of giving the boundary values at a point (x,h ), we use a Taylor series expansion
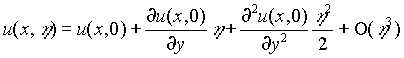 .
.
The disadvantage is that the boundary conditions are more complicated, but the simplicity of a regular domain outweighs this problem.
A comparison with some experimental results using Pseudomonas aeruginosa in a straight tube, and using oxygen as the limiting nutrient was done in Cunningham, et al. Results agree to 10-20%.
Microscopic models, such as the one described above, help understand the basic biofilm growth processes, help determine parameters that are hard or impossible to measure, and complement experiments. More complete models are in development.
Homogenization
Porous media are very complicated. It is not possible to simulate the flow at each pore. In order to obtain results at the macroscopic scale, some sort of averaging needs to be done. Homogenization (Bensoussan, et al., 1978) is a formal mathematical technique for averaging the microscopic equations and obtaining macroscopic descriptions of the porous medium. It has been successfully used to rederive Darcy's law from the Navier-Stokes equations, for both single and multiple-phase fluids (Keller, 1980; Bourgeat, et al.,1988).
Homogenization consists of assuming that the problem has two different length scales, a short and a long one. Supposing that every variable depends on those two scales, a perturbation expansion in the ratio of those two scales is then done, making sure that seculars (terms that are not bounded) are canceled. The resulting equations are then averaged to eliminate the small scale. One additional assumption is the periodicity in the small scale. The application of the method to general nonlinear problems is still not well understood.
Here we apply homogenization to the transport equation with different reaction terms for the interaction between the biofilm and nutrients or pollutants. The derivation is first done in one dimension and then in two and three.
Consider first the diffusion-reaction equation
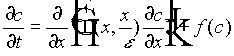 , (9)
, (9)
where f(c) is a reaction term, for example given by Monod kinetics. x is the macroscopic length; 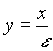 is the microscopic length; and e
is the ratio of the pore scale l to the macroscopic scale L.
is the microscopic length; and e
is the ratio of the pore scale l to the macroscopic scale L.
Next we expand each of the variables as an asymptotic series in e . For example, c(x,y,t,e ) is
![]() . (10)
. (10)
The x-derivative is replaced by
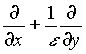 . (11)
. (11)
Substituting (10) and (11) into (9), and by grouping terms in powers of e , we obtain a hierarchy of equations. The first three are
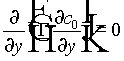 (12)
(12)
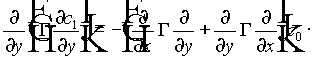 (13)
(13)
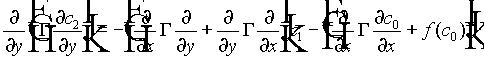 (14)
(14)
If we impose boundedness conditions on ![]() , we obtain that
, we obtain that ![]() ; and on
; and on ![]() , we obtain, the following equation
, we obtain, the following equation
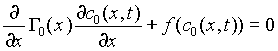 , (15)
, (15)
where
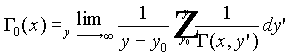 .
.
This limit is independent of the choice of ![]() .
.
By solving (15) we have, to lowest order, the value of the concentration. An advection term and more equations to solve for bacterial interaction with nutrients can be added and the procedure is similar. For more details see Desai and Chen, 1995.
Porosity and permeability
In order to determine the effect of biofilms on plugging the porous medium, it is necessary to determine the effect of bacterial growth on porosity and permeability. Using the microscopic model, it is possible to determine the change in the tube volume occupied by the bacteria. Calculations can be done in tubes with expansions and contractions to simulate some tortuosity. The permeability is then determined from empirical relations or from relations that assume a simple pore geometry, such as networks of straight tubes or packed beds of uniform spheres.
Knapp, et al. 1988, give the following relation between the reduction of permeability of a porous medium and the reduction of porosity due to bacterial plugging of the medium:
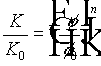 ,
,
where K and f are the permeability and porosity, and the subindex 0 refers to the initial value, n is an experimentally determined parameter, which is around three. Several other formulas are given by Bear, 1972.
Conclusions
We have presented a microscopic model to simulate biofilm growth inside a porous medium. This model is useful in simulating a variety of hypotheses . We have also presented how homogenization is used to scale results from the pore scale into the lab scale, and to obtain values that are averages of the microscopic ones. Finally, we have given some relations between amount of biomass and macroscopic properties such as porosity and permeability. Work is ongoing on all three topics to construct better models.
Acknowledgment
Although this article has been funded in part by the U.S. Environmental Protection Agency under the assistance agreement R-819653, through the Great Plains/Rocky Mountain Hazardous Substance Research Center headquartered at Kansas State University, it has not been subjected to the agency’s peer and administrative review and therefore may not necessarily reflect the views of the agency, and no official endorsement should be inferred.
References
Ames, W.F., 1992, Numerical Methods for Partial Differential Equations, Academic Press Inc., Boston.
Baker, K.H. and D.S. Herson, 1994, Bioremediation, McGraw-Hill, New York.
Bear, J., 1972, Dynamics of Fluids in Porous Media, American Elsevier, New York.
Bensoussan, A., J.L. Lions and G. Papanicolau, 1978, Asymptotic Analysis for Periodic Structures, North-Holland, Amsterdam.
Bourgeat, A., M. Quintard and S. Whitaker, 1988, Eléments de comparison entre la méthode d’homogénésation et la méthode de prise de moyene avec fermature, C.R. Acad. Sci. Paris, 306.
Characklis, W.G. and K.C. Marshall, 1990, Biofilms: A basis for an interdisciplinary approach. In: W.G. Characklis and K.C. Marshall, Eds., Biofilms, Wiley-Interscience, New York.
Chen, B., A. Cunningham and E. Visser, 1996, Numerical simulation of biofilm growth in porous media at the microscale, in Computational Methods in Water Resources XI, eds. A.A. Aldama, et al., Computational Mechanics Publications, Southampton.
Cunningham, A.B., E. Visser, Z. Lewandowski and M. Abrahamson, 1995, Evaluation of a coupled mass transport-biofilm process model using dissolved oxygen microsensors, Water Sci. and Tech. 32.
Desai, A. M. and B. Chen, 1996, Homogenization analysis applied to transport in heterogeneous porous media, Proc. of the 16th Annual American Geophysical Union Hydrology Days, ed. H. J. Morel-Seytoux, Hydrology Days Publications, Atherton, CA.
Gujer, W. and O. Wanner, 1990, Modeling mixed population biofilms. In: W.G. Characklis and K.C. Marshall, Eds., Biofilms, Wiley-Interscience, New York.
Keller, J., 1980, Darcy’s law for flow in porous media and the two-space method. In: R.L. Sternberg, A.J. Kalinowski and J.S. Papadakis, Nonlinear Partial Differential Equations in Engineering and Applied Science, Marcel Dekker, New York.
Kincaid, D.R. and E.W. Cheney, 1991, Numerical Analysis, Brooks/Cole Publishing Co., Pacific Grove, CA.